Anyway, my numbers were way off. I thought I was doing it right, but I must've been entering something incorrectly. I finally gave up and used the formula that Excel has just for this sort of thing, and which Jackalware originally used as well.
Here's what the results look like:
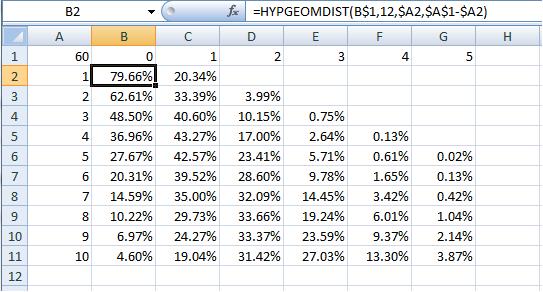
How do you read this?
The "60" in the upper left is the number of cards in the deck.
The rest of the numbers in column A represent how many of card "X" you have in the deck (terrain, shields, Vampires, Knights, etc.).
The rest of the numbers in row 1 represent how many you may get in your initial 12 card draw.
The formula is shown. Note the dollar signs ($). They are important for cutting and pasting in Excel. Don't forget them. Notice that $A$1 has two of them. Doubly important.
You can expand the list by adding more rows and columns and copying & pasting the formula into more cells. It you paste into an invalid cell (e.g., drawing 3 copies of a card when there are only 2 in the deck), you will get an error.
The formula has a 12 in it. That stands for the 12-card draw.
You can adjust this for other card games (do you play other card games?) just by changing that number.
How NOT TO read this
Let's say you have 8 Shields and 8 Terrain in a deck of 60 cards.
There is a 33.66% chance of getting 2 Shields in the initial draw.
There is a 33.66% chance of getting 2 Terrain in the initial draw.
There is NOT a 67.32% chance of getting 2 Shields and 2 Terrain!
Nor if there a (33.66*33.66)% chance. (In other words, don't add or multiply).
It's a little more complicated than that.
The chart just gives you a basic idea, such as if you put 8 in your deck, you are most likely to get 1 or 2. If you put 10 in your deck, you are likely to get 2 or 3.
If you 5 each of 8 creatures, you will most likely get 1 of any specific one, but you could easily get 2 of some and none of the others.










2 comments:
I like the way you have laid this out visually...I never thought of doing that. Very nice!
I'll have to work on part 2 soon...
Glad you liked it.
I seriously thought that I could handle the math without using the formula, and if I didn't know that the formula existed, I would have eventually found my mistake. Most likely.
But once you know it's available, it's hard not to just go the easy way.
Post a Comment